Perbedaan estimasi sumber daya menggunakan metode Kriging dan Inverse Distance Weighting (IDW) antara lain:

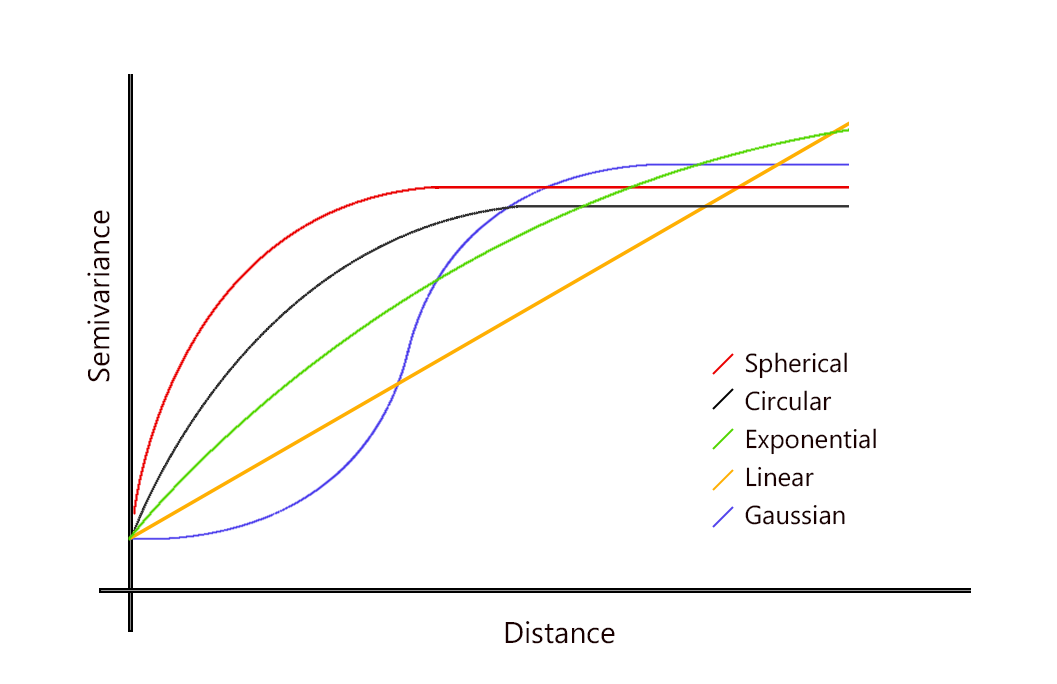
1. Dasar teori: Metode Kriging memodelkan korelasi spasial antar titik pengamatan, sedangkan metode IDW memperhitungkan jarak spasial antara titik pengamatan.
2. Penggunaan data: Metode Kriging membutuhkan data variogram untuk menentukan model spasial, sedangkan metode IDW hanya membutuhkan data pengamatan.
3. Keakuratan estimasi: Estimasi yang dihasilkan oleh metode Kriging lebih akurat karena mempertimbangkan struktur spasial data, sedangkan estimasi yang dihasilkan oleh metode IDW tergantung pada parameter smoothing radius yang digunakan.
4. Variabilitas estimasi: Variabilitas estimasi yang dihasilkan oleh metode Kriging rendah karena mempertimbangkan korelasi spasial, sedangkan variabilitas estimasi yang dihasilkan oleh metode IDW tinggi karena tidak mempertimbangkan korelasi spasial.
5. Robustness: Metode Kriging kurang tahan terhadap data outliers, sedangkan metode IDW lebih tahan terhadap data outliers.
6. Komputasi: Metode Kriging memiliki komputasi yang lebih kompleks dan memerlukan waktu yang lebih lama, sedangkan metode IDW memiliki komputasi yang lebih sederhana dan memerlukan waktu yang lebih singkat.

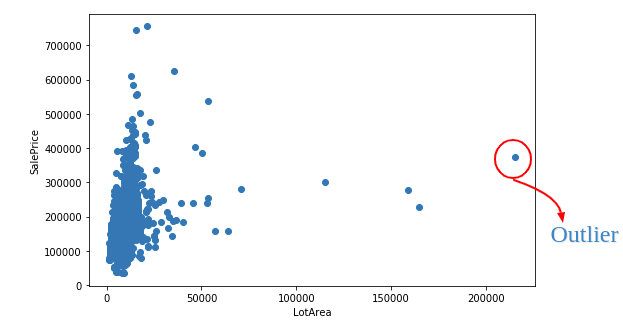
Data outliers atau pencilan adalah data yang jauh berbeda dari data lainnya dalam kumpulan data. Pencilan dapat terjadi karena beberapa alasan, seperti kesalahan pengukuran, kesalahan entri data, atau kondisi yang tidak biasa dalam sampel yang diambil. Pencilan dapat mempengaruhi analisis data, termasuk dalam melakukan estimasi sumber daya, sehingga perlu diperhatikan dan diatasi dengan tepat.

Dalam melakukan analisis data, ada beberapa cara untuk mengatasi data outliers, antara lain:

1. Menghapus data outliers: Cara paling sederhana adalah dengan menghapus data outliers dari kumpulan data. Namun, cara ini harus dilakukan dengan hati-hati, karena dapat mengubah hasil analisis secara signifikan.
2. Transformasi data: Transformasi data dapat dilakukan untuk mengurangi pengaruh data outliers. Salah satu cara yang umum dilakukan adalah transformasi logaritmik.
3. Menggunakan metode robust: Metode robust adalah metode yang dirancang untuk mengatasi data outliers. Contoh metode robust adalah metode Median Absolute Deviation (MAD) dan metode Least Trimmed Squares (LTS).
4. Menggunakan metode yang tidak sensitif terhadap data outliers: Beberapa metode analisis data, seperti metode K-nearest neighbors dan metode Decision Trees, tidak sensitif terhadap data outliers.

Dalam melakukan estimasi sumber daya, data outliers dapat mempengaruhi hasil estimasi yang dihasilkan oleh metode. Oleh karena itu, sebelum melakukan estimasi sumber daya, perlu dilakukan pengolahan data untuk mengatasi data outliers. Salah satu cara yang dapat dilakukan adalah dengan menggunakan metode robust atau metode yang tidak sensitif terhadap data outliers.

Ada beberapa indikator statistik yang dapat digunakan untuk mengidentifikasi data outlier, yaitu:

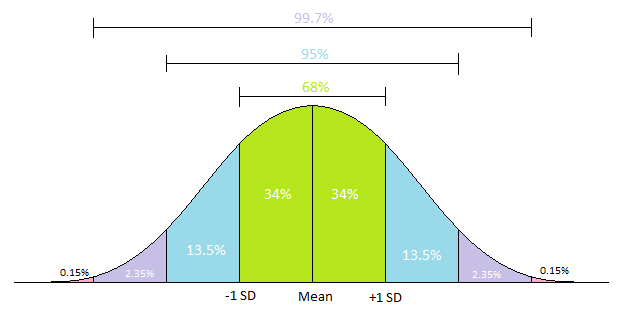
1. Mean dan Standar Deviasi Indikator statistik ini dapat digunakan untuk mengidentifikasi data outlier pada data yang berdistribusi normal. Data outlier dianggap sebagai data yang memiliki nilai jauh dari nilai mean, dengan jarak yang lebih dari 2 atau 3 standar deviasi.
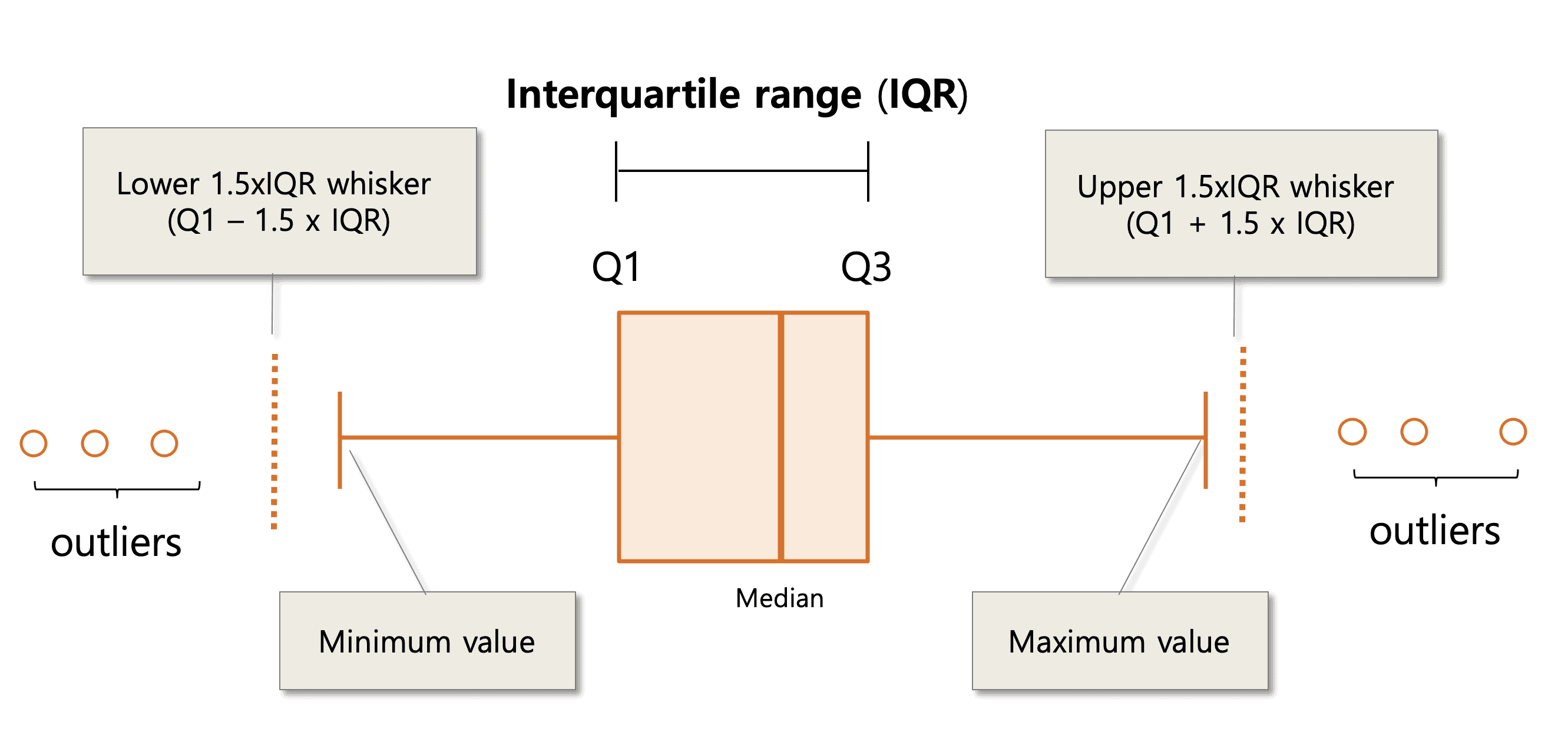
2. IQR (Interquartile Range) IQR adalah jarak antara kuartil atas dan kuartil bawah pada data. Data outlier dianggap sebagai data yang memiliki nilai lebih besar dari kuartil atas ditambah 1,5 kali IQR atau nilai lebih kecil dari kuartil bawah dikurangi 1,5 kali IQR.
3. Z-score Z-score adalah jarak antara nilai observasi dengan nilai mean dalam satuan standar deviasi. Data outlier dianggap sebagai data yang memiliki z-score lebih besar dari 2 atau lebih kecil dari -2.
4. Box Plot dapat digunakan untuk memvisualisasikan data outlier. Data outlier dianggap sebagai data yang memiliki nilai di luar rentang antara kuartil atas dan kuartil bawah yang ditandai dengan adanya titik-titik atau simbol-simbol pada box plot.
   
5. Grubbs’ Test Grubbs’ Test adalah uji statistik yang digunakan untuk menguji keberadaan data outlier pada data yang berdistribusi normal. Data outlier dianggap signifikan jika nilai t-statistik lebih besar dari nilai kritis yang tergantung pada jumlah data dan tingkat kepercayaan yang digunakan.

Rumus Inverse Distance Weighting (IDW) adalah sebagai berikut:

Z(x) = Σ [w(i) x Z(i)] / Σ w(i)

Di mana:

• Z(x) adalah nilai yang akan diestimasi di lokasi x
• Z(i) adalah nilai observasi di titik i
• w(i) adalah bobot yang diberikan ke observasi i, dihitung dengan rumus:

w(i) = 1 / [d(x, i)]^p

Di mana:

• d(x, i) adalah jarak antara lokasi x dengan titik i
• p adalah parameter penghalus yang dapat diatur oleh pengguna untuk menentukan seberapa cepat bobot berkurang dengan meningkatnya jarak. Semakin besar nilai p, semakin cepat bobot menurun dengan meningkatnya jarak.

Rumus dasar Kriging adalah sebagai berikut:

Z(x) = μ + Σ λ(i) [Z(i) – μ]

Di mana:

• Z(x) adalah nilai yang akan diestimasi di lokasi x
• μ adalah nilai rata-rata dari variabel yang diestimasi
• Z(i) adalah nilai observasi di titik i
• λ(i) adalah bobot Kriging yang diberikan pada nilai observasi di titik i

Bobot Kriging dihitung berdasarkan persamaan sistem persamaan linear yang terdiri dari persamaan struktur varians dan persamaan kovariansi cross:

• Persamaan Struktur Varians: C(0) = Var(Z(x)) – Σ λ(i) Cov(Z(i), Z(x))
• Persamaan Kovariansi Cross: C(h) = Cov(Z(x), Z(x+h)) – Σ λ(i) Cov(Z(i), Z(x+h))

Di mana:

• C(0) adalah varians yang diperkirakan pada titik yang akan diestimasi
• C(h) adalah kovariansi yang diperkirakan antara titik yang akan diestimasi dengan titik lain pada jarak h
• Var(Z(x)) adalah varians sebenarnya dari variabel pada titik yang akan diestimasi
• Cov(Z(i), Z(x)) adalah kovariansi antara variabel pada titik i dengan variabel pada titik yang akan diestimasi
• Cov(Z(i), Z(x+h)) adalah kovariansi antara variabel pada titik i dengan variabel pada titik yang berjarak h dari titik yang akan diestimasi.

Bobot Kriging dapat dihitung dengan meminimalkan varians estimasi, yaitu dengan menggunakan persamaan:

minimize: C(0) – Σ λ(i) C(h)

Sistem persamaan linear ini dapat dipecahkan untuk mendapatkan bobot Kriging dan kemudian digunakan untuk menghitung nilai estimasi pada lokasi yang akan diestimasi.

Dalam memilih metode yang tepat untuk melakukan estimasi sumber daya, perlu dipertimbangkan karakteristik data dan tujuan analisis yang ingin dicapai. Kedua metode memiliki kelebihan dan kelemahan masing-masing, sehingga pemilihan metode yang tepat harus dilakukan berdasarkan kebutuhan spesifik dari analisis data spasial yang dilakukan.